Mesterséges idegsejtek: hogyan írják le a matematikusok az idegsejtek jelfeldolgozását?
Az #agyséta előző cikkeiben egyszerűen, majd részletekbe menően is átvettük, hogy egy biológiai idegsejt hogyan összegzi a rá érkező ingerületeket és a kiváltott válasz jel hogyan terjed. Most azt mutatom be hogyan lehet egyszerű matematikai leírását adni egy idegsejt jelintegrációjának. Sajnos sokan ódzkodnak a matematikától, pedig tudni kell, a matematikus alapjában lusta, mindig a legegyszerűbb leírását próbálja adni egy problémának. Sokan ott buknak el, hogy ehhez a matematikus a saját nyelvét, a képletekkel leírt egyenleteket használja.
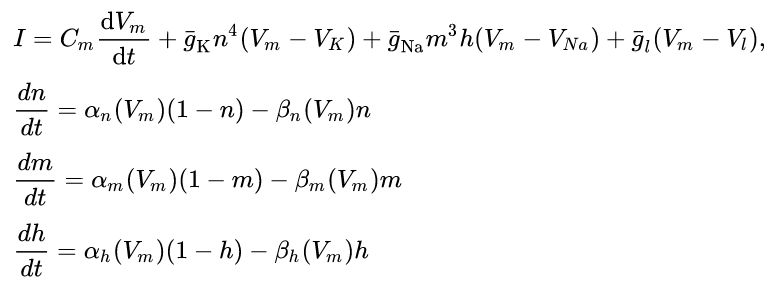
Az idegsejtek vizsgálatának hőskorában a biológusok megfigyeléseit a matematikusok és fizikusok igyekeztek egyenletek formában megragadni. A fenti hihetetlenül bonyolult fizikai kémiai folyamatokat sikerült Hodgkin-nak és Huxley-nak differenciál egyenletekkel leírni, amit Nobel díjjal jutalmaztak 1963-ban. Ez egy pontos, de még mindig bonyolult leírása volt az idegsejtek működésének.
A számunkra emészthetőbb leírást McCulloch és Pitts alkotta meg 1943-ban (MCP modell). Ez volt az első mesterséges idegsejt (neuron) modell. Mindössze ennyi:
Ugye minden modell, így az idegsejtmodell is, a valóság leegyszerűsítése, hogy bizonyos kérdésekre hatékonyabban és/vagy egyszerűbben lehessen válaszolni. Persze mint minden modellnél, tisztában kell lennünk azzal mit építünk be, mit dobunk ki. Ez be is határolja, hogy mit kérdezhetünk (és fordítva, a kérdés szabja meg mennyire egyszerűsítünk). A mesterséges ideghálózatok és az általuk használt idegsejtek esetében nem a biológiai hűség, hanem a tömör matematikai leírás a cél, hogy könnyen számolhassuk az elemek működését és hatékonyabban tudjunk számítógépeken mesterséges idegsejteket és idegsejt hálózatokat szimulálni (vizsgálni). A mesterséges idegsejt és hálózat modellek a skála egyik végén álló egyszerű MCP sejttől a biológiai sejtre igen hasonló összetett jelintegráló modell rendszerig folyamatos skálát alkotnak.
De fordítsuk le mi van odafent a legegyszerűbb leírásban. Egy idegsejt számos (~10,000) bemenetet kap más sejtek axonvégződéseitől. Az axonokon érkező bemenetek értékét az x1, x2, …x10000 változókban tárolhatjuk egy modellben. Hogy az axonon érkező bemenet milyen erősen adódik át a beidegzett sejt dendritjére, azaz azt a szinapszis mennyire erősíti, a w1, w2, … w10000 változókban található (szinaptikus súlyok, az angol weight=súly rövidítése) tartalmazzák. A ∑ (nagy szigma, jelentése szumma) azt jelenti, hogy ahhoz, hogy a sejtre érkező bemenetet megkapjuk, össze kell adnunk az összes bemenetre a bemenet értékét megszorozva a szinaptikus súllyal (x1*w1)+(x2*w2)*….(x10000*w10000). Hiszen a sejttesten a dendritekből érkező áramok összegződnek. A második egyenlet pedig azt jelenti, hogyha az összeg, u, nagyobb, mint a küszöb Θ (theta az angol threshold = küszöb görög rövidítése), akkor a sejt kimenete, y, 1 lesz különben marad 0 (a valódi idegsejt esetében kisül a sejt vagy nem).
Ezen egyenletek alapján viszonylag alacsony számításigénnyel lehetett hatékonyan számolni kis neuronhálózatok működését. Bár ekkor még nem léteztek számítógépek. Ezek elméleti megalapozását Alan Turing elmélete alapján Neumann János dolgozta ki az EDVAC jelentésben.
Az agy és a számítógép kapcsolatának érdekes csavarjaként az első általános célú számítógép elemeinek megtervezésénél Neumann felhasználta McCulloch és Pitts absztrakt neuronjait. Nem is csoda, hiszen egy kevés bemenettel rendelkező idegsejt jelintegrációja nem áll messze egy logikai művelet elvégzésétől. Ha sejtünknek két bemenete van és aktiválódási küszöbe 2 akkor az ÉS (AND) logikai műveletet képes elvégezni, azaz csak akkor lesz aktív, ha mindkét bemenete aktív. Ha a sejt aktiválódási küszöbe csak 1, akkor bármely bemenet aktiválódása esetén aktív lesz, azaz egy VAGY (OR) műveletet végez. Egy NEM (NOT) logikai műveletet pedig egy egyetlen bemenetű, 1 küszöbű gátlósejttel lehet leírni. Ennek a 3 elemnek a használatával pedig bármely logika függvényt fel lehet építeni egy kis neuronhálózatból.
Ilyen neuronokból építette fel terveiben Neumann a feldolgozó egység összeadó, szorzó, osztó, gyökvonó és egyéb elemeit, illetve a memóriát és a vezérlést. Utána pedig a mérnökök tranzisztorokból alakították ki az idegsejtek számításain alapuló logikai kapukat.
A legegyszerűbb idegsejt modellt (MPC) „integrate and fire” modellnek hívják (összegyűjt és aktiválódik). Az elméleti szakemberek hamar rájöttek arra, hogyha az idegsejtek kimenete nem bináris [0 vagy 1] hanem folytonos [0 és 1 közötti], illetve, ha a válaszfüggvénye (az összegzett áram hogyan alakul válasszá) nem egy hirtelen ugrás 0ról 1re, hanem egy nemlineáris függvény, akkor sokkal kifinomultabb számításokra képes egy modell idegsejtekből álló hálózat. A folytonos esetet biológiában úgy lehet elképzelni, hogy a sejtnek nem csak tüzel/nem tüzel állapota van, hanem különböző gyakorisággal (frekvenciával) is bocsájthat ki akciós potenciálokat. A nemlineáris pedig azt jelenti, hogy kétszer, négyszer akkora bemenő jelre nem kétszer, négyszer akkora lesz a válasz, hanem ennél nagyobb (supralineáris, vagy kisebb (sublineáris).
A fizikában az ilyen nemlineáris bemenet-kimenet esetre leggyakrabban a sigmoid függvényt (görbét) használják. Történetesen az idegsejtek is ilyen szigmoid aktiválódási küszöbbel bírnak. A szigmoid görbe egy ideig vízszintesen fut minimális értékén (nem változik), aztán egy küszöbértéknél elkezd emelkedni, az egyedi görbékre jellemző meredekséggel fut felfelé, majd újra kilaposodik a maximális értéknél.
Ezen a ponton (valahol az 1960as években) aztán hosszú időre el is vált egymástól a fizikusok és agykutatók útja. A kezdeti ihlet után a fizikusok rengeteg dologra kezdték el használni a formális neuronokat és mindenféle ravasz módosításokat eszközöltek azért, hogy hálózataik jobban viselkedjenek (azaz bonyolultabb és gyorsabb számításokat tudjanak kiegyensúlyozottan elvégezni). Megjelentek olyan „neuronhálózatok” amelyek már igencsak elrugaszkodtak a valós biológiai alapelvektől. Kialakultak egzotikus nevű megoldások, mint például a Perceptron.
Az egyik ilyen újítás volt a „backpropagation”- visszaterjedés. Itt az idegsejtek nyúlványrendszerén a jel nem csak a biológiában megengedett szinapszis->dendrit->sejttest->axon irányba terjedhet, hanem visszafelé is. Ebben a rendszerben speciális szinaptikus tanulási szabályokat is beépítettek, ami az agyban nem található meg. A másik, biológiailag nem helyes megoldás az volt, hogy egy sejtnek nemcsak pozitív, hanem negatív szinaptikus súlyai is lehettek, azaz bizonyos kimenetei serkentők, mások gátlók voltak, sőt ezek át is válthattak egymásba. Mint írtam, az agykéregben az idegsejt típusa határozza meg hogy serkentő vagy gátló kapcsolatokat alkot axonterminálisaival. Mivel, mint majd a későbbiekben látni fogjuk, a két sejttípus alapvetően más szerepet tölt be az információ feldolgozásában.
Az eltérésekbe itt most nem megyünk bele, mert a tanulásról és sok másról majd a következő részben a hálózatoknál lesz szó. Ott pillantást vetünk majd a modell idegsejtekre és hálózatokra is, illetve, hogy amikor a mesterséges intelligencia kutatók újra az agykutatókhoz fordultak ihletért, miket vettek ám ami a jelenlegi Deep Learning AI forradalomhoz vezetett.
Szerző: Gulyás Attila