Hálózatok két szinten: nem minden agyi hálózat skálafüggetlen
A megígért makákó előtt még egy kis elméleties kitérő.
Mielőtt továbbmegyünk az #agysétával, üssük bele az orrunkat egy kicsit a manapság igen népszerű és sok mély belátásra vezető hálózatelméletbe, mely Barabási-Albert László munkássága kapcsán került a mindennapi nyelvezetbe. A hálózatelmélet a matematika egyik ágának a gráfelméletnek a része.
A gráfelmélet összekapcsolt pontokból álló struktúrák tulajdonságait vizsgálja. Egy gráfot (magyarul hívhatjuk hálózatnak) a matematikusok és a fizikusok (csomó)pontokkal és a pontok között futó kapcsolatokkal (élekkel) írnak le. Ugye az agy idegsejtek hálózata, azaz hálózat, azaz az agy szerkezete is vizsgálható gráfelmélettel és az ennek részét képező hálózatelmélettel. Ezt sokan, elsősorban nem biológusok meg is tették nagy lelkesedéssel.
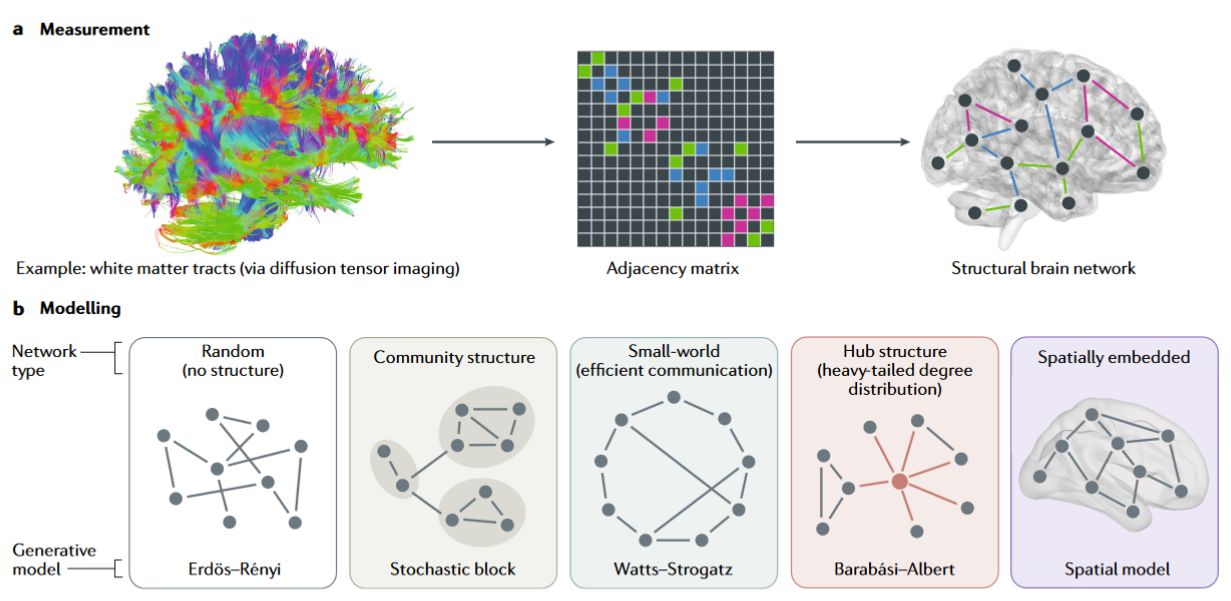
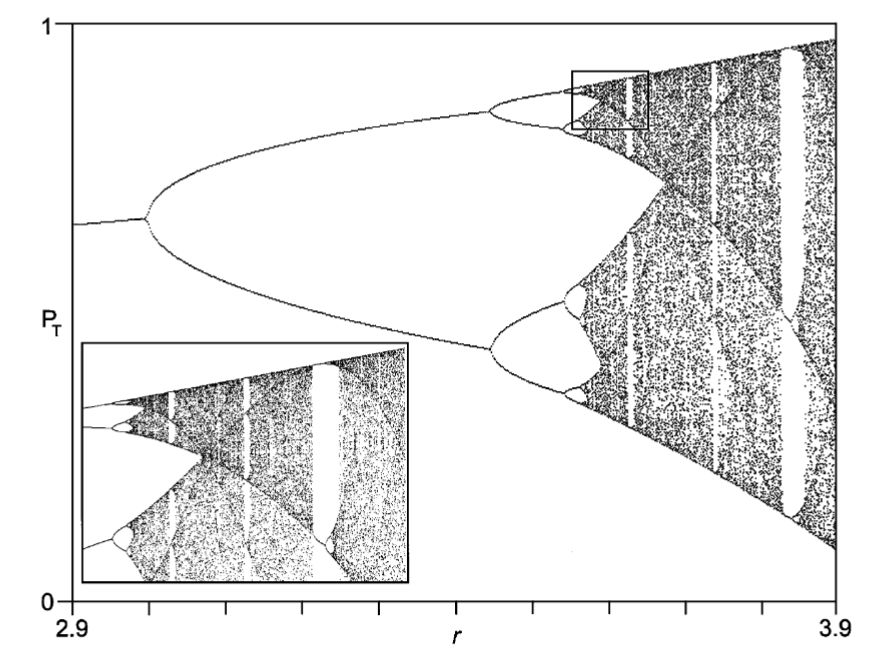 Itt én most kicsit kotnyeleskedek, de az igazat megvallva a fizikusok/matematikusok is ezt teszik az aggyal. Hasznosak az ilyen határtudományi kotnyeleskedések, de általában finomításra szorulnak a másik oldal részéről. Barabási nyomán, az elmúlt években sokat hallhattunk a skála független hálózatokról (legyen SFH, angolul scale free network). Hasznos idea, sok mindent lehet vele magyarázni, de mint ahogy minden aktuális üdvmódszerrendszert mindenre ráhúznak (a természettudományokban a fizikusok haljanak erre, hiszen ők foglalkoznak a világ struktúráival, voltak már ugye káosz, fraktál és egyéb korszakok), ezt is felületesen ráhúzták az agy működésére, pontosabban az agy összeköttetés rendszerére. Így utólag javítanék egy kicsit, és tisztába tenném hol vannak és hol nem az agy esetében SFH-k.
Itt én most kicsit kotnyeleskedek, de az igazat megvallva a fizikusok/matematikusok is ezt teszik az aggyal. Hasznosak az ilyen határtudományi kotnyeleskedések, de általában finomításra szorulnak a másik oldal részéről. Barabási nyomán, az elmúlt években sokat hallhattunk a skála független hálózatokról (legyen SFH, angolul scale free network). Hasznos idea, sok mindent lehet vele magyarázni, de mint ahogy minden aktuális üdvmódszerrendszert mindenre ráhúznak (a természettudományokban a fizikusok haljanak erre, hiszen ők foglalkoznak a világ struktúráival, voltak már ugye káosz, fraktál és egyéb korszakok), ezt is felületesen ráhúzták az agy működésére, pontosabban az agy összeköttetés rendszerére. Így utólag javítanék egy kicsit, és tisztába tenném hol vannak és hol nem az agy esetében SFH-k.
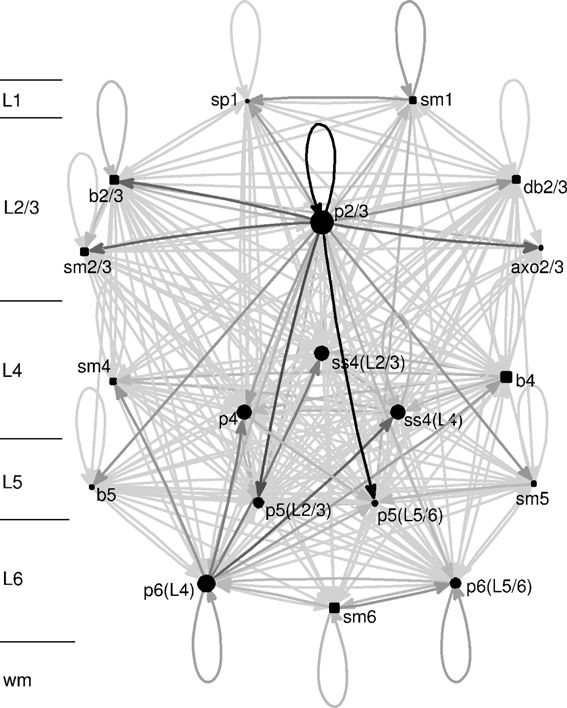 Fontos, hogy az agyban két hálózati szint van, a kishálózatok szintje (második lépésünkben érintettük) és az agyi területek hálózatba kapcsolt hálózatainak szintje (harmadik lépésünkben fogjuk érinteni). E két hálózati szint teljesen más hálózati leírást igényel, az SFH leírás nem alkalmazható az alacsonyabb szintre, csak, (részben) a magasabbra.
Fontos, hogy az agyban két hálózati szint van, a kishálózatok szintje (második lépésünkben érintettük) és az agyi területek hálózatba kapcsolt hálózatainak szintje (harmadik lépésünkben fogjuk érinteni). E két hálózati szint teljesen más hálózati leírást igényel, az SFH leírás nem alkalmazható az alacsonyabb szintre, csak, (részben) a magasabbra.
Az alacsonyabb szinten, a kis hálózatokban viszonylag szigorú szabályok szerint lépnek kapcsolatba a serkentő (S) sejtek, a gátlósejtek (G) és a két csapat egymással. Ezek leírására nemigen használható a SFH megközelítés, mert 1) egy kishálózaton belül két tetszőleges sejt, között hálózatelméleti értelemben kb. ugyanolyan távolság van (ugyanannyi szinaptikus kapcsolaton keresztül éri el egymást két sejt), 2) minden sejt hasonló mennyiségű másikkal van összekötve, azaz nincsenek, kiemelkedően sok kapcsolattal rendelkező, bennfentes „hub” és marginalizált, magányos sejtek. Agyterülete válogatja, hogy egy sejt hány másikkal kapcsolódik (6-35 ezer között mozog), azaz milyen valószínűséggel lép kapcsolatba tetszőleges másik sejttel. Ezek a valószínűségek kicsit mások a S-S, G-G, G-S és S-G kapcsolatok esetében, de mindenesetre nem mutatják a SFH-ra jellemző jellegzetes eloszlásokat.
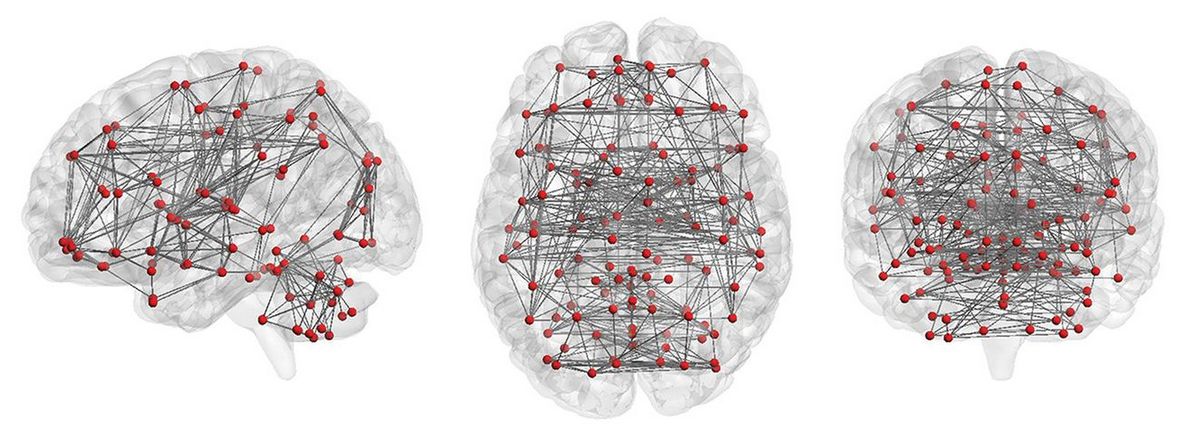 A hálózatosság magasabb szintjén, ahol különböző agyterületek kapcsolódnak egymáshoz, már alkalmazható a SFH-k ötlete. Itt ugyanis vannak kevés és sok kapcsolattal rendelkező agyterületek a hierarchia különböző szintjein. A hamarosan sokat emlegetésre kerülő hippokampusz, amigdala és főleg a homloklebeny bizonnyal pályázhat a hub pozíciójára. Bár óvatosnak kell lenni itt is, mert bár az agyban sok agyterület kapcsolódik össze sok másikkal, azaz sok hálózati csomópont és sok összeköttetés (él) van benne, ezek száma azért jóval alacsonyabb, mint a Barabási által tanulmányozott rendszerekben (pl. szociális hálók) ezért nehezebb kapcsolat-eloszlást számolni, mely támogatná a SFH elképzelést.
A hálózatosság magasabb szintjén, ahol különböző agyterületek kapcsolódnak egymáshoz, már alkalmazható a SFH-k ötlete. Itt ugyanis vannak kevés és sok kapcsolattal rendelkező agyterületek a hierarchia különböző szintjein. A hamarosan sokat emlegetésre kerülő hippokampusz, amigdala és főleg a homloklebeny bizonnyal pályázhat a hub pozíciójára. Bár óvatosnak kell lenni itt is, mert bár az agyban sok agyterület kapcsolódik össze sok másikkal, azaz sok hálózati csomópont és sok összeköttetés (él) van benne, ezek száma azért jóval alacsonyabb, mint a Barabási által tanulmányozott rendszerekben (pl. szociális hálók) ezért nehezebb kapcsolat-eloszlást számolni, mely támogatná a SFH elképzelést.
Legközelebb már tényleg a makákó jön.
Szerző: Gulyás Attila





